Показатели центральной тенденции

Средние величины применяют в случае, если нужно отразить в одном значении особенности набора данных. Так при всем разнообразии размеров признака у отдельных обьектов в их совокупности существуют характерные для данных конкретных условий размеры этого признака. Например, при всем разнообразии урожайности пшеницы на отдельных гектарах в хозяйстве существует какой-то уровень урожайности, присущий именно данному хозяйству. Отличительной особенностью статистических средних является то, что в них взаимно погашаются индивидуальные различия признака у отдельных единиц изучаемой совокупности, в результате появляется возможность охарактеризовать общие черты и свойства массовых явлений, закономерности их развития.

Средние величины также часто используются для расчетов других статистических показателей.

Среднеарифметическое.

Среднеарифметическое является, вероятно, наиболее употребляемой из всех видов средних величин. Оно часто называется просто "средней". В формулах среднеарифметическое обозначается в виде x.   Формула для расчета среднеарифметического набора данных:

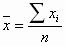
Медиана.

Медиана является еще одним часто применяемым видом средней. Она особенно подходит для описания асимметрично распределенных данных. Медиана буквально означает середину. Медианой будет являться среднее значение набора данных, упорядоченных по возрастанию. Точнее, медиана это значение, делящее набор данных на две половины, одна из которых состоит из наблюдений больше значения медианы, а другая - из значений меньших медианы.

Еще о средних

Показатели варьирования или разброса.

Глядя на график (см. ниже) частотного распределения приблизительно нормально распределенных данных можно заметить две характерные особенности: 1) кривая имеет пик, обычно недалеко от центра и 2) кривая плавно спадает по обе стороны от пика. Подобно тому, как средние величины использовались для описания местоположения пика, показатели варьирования указывают насколько велик разброс (варьирование) данных вокруг центрального значения. Существует несколько показателей варьирования.

Процентили, квартили и межквартильный размах.

Максимальное значение частотного распределения можно рассматривать как такое значение набора данных, с которым совпадают или являются меньше него 100% наблюдений. Когда максимальное значение рассматривают таким образом, его называют сотым процентилем. Используя такой же подход, говорят, что медиана, с которой совпадают или являются меньше ее 50% данных, является 50-ым процентилем. N-ым процентилем распределения называется значение, с которым совпадают или находятся ниже N процентов данных. Помимо медианы часто используются 25-й и 75-й процентили. 25-й процентиль называется также первым квартилем, медиана или 50-й процентиль является одновременно вторым квартилем, 75-й процентиль ретьим, а 100-й процентиль соответственно является четвертым квартилем. Межквартильный размах представляет собой центральную часть распределения и подсчитывается как разность между третьим и первым квартилями. В этом диапазоне лежит примерно половина набора нормально распределенных данных, вне его с каждой стороны находится примерно по четверти наблюдений.

Дисперсия, стандартное отклонение, коэффициент вариации.

Если вычесть среднеарифметическое из каждого наблюдения, сумма полученных разностей будет равна 0. Эта идея вычитания средней из каждого наблюдения лежит в основе расчета двух показателей варьирования и стандартного отклонения. Для получения этих показателей разности возводятся в квадрат с целью устранения отрицательных чисел. Затем квадраты разностей складываются и делятся на n для нахождения "среднего" квадрата разности. Такая "средняя" величина называется дисперсией и обозначается латинской буквой s² - сигма. Чтобы вернуться к первоначальной размерности, из s² (значения дисперсии) извлекается квадратный корень. Квадратный корень из дисперсии называется среднеквадратическим или стандартным отклонением.   Коэффициент вариации - относительный показатель варьирования, численно равный отношению стандартного отклонения к средней.

Статистические выводы.

Средние значения и показатели разброса часто рассчитываются для описания конкретного набора данных. Однако в других случаях, когда данные представляют собой выборку из генеральной совокупности бывает необходимо экстраполировать выводы, сделанные на основании анализа выборки, на всю совокупность, из которой эта выборка была взята. Такую экстраполяцию выводов называют статистическими выводами. Известно большое число статистических методов, позволяющих сделать эти выводы. Когда делается вывод исходя из нормально распределенных данных, заключение основывается на отношении стандартного отклонения и среднего и нормальной кривой. Эти отношения, иллюстрируемые на рисунке, используются при получении выводов.

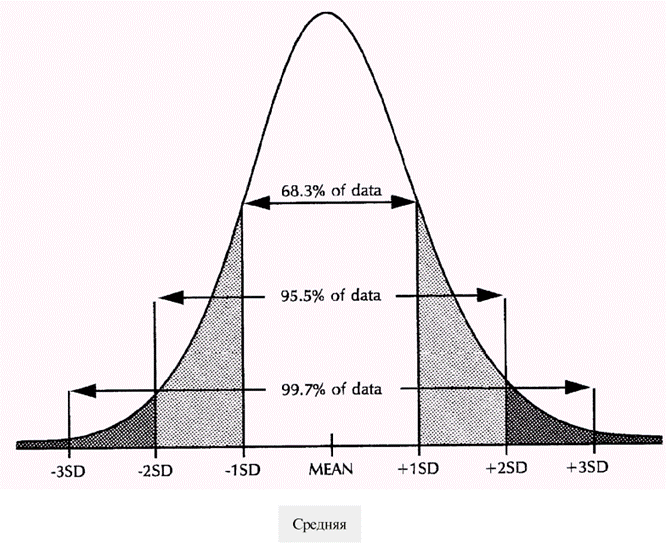
Если график распределения данных похож на нормальную кривую, предполагают, что генеральная совокупность, из которой были получены данные выборки, нормально распределена. Затем предполагают, что если бы имелись все возможные наблюдения из этой выборки, обнаружилось бы, что 68,3%, 95,5% и 99,7% совокупности лежит между средней и +/- 1, +/- 2 и +/- 3 стандартных отклонений соответственно. Также предполагается, что 95% совокупности лежит между средней и +/- 1,96 стандартных отклонений.

t-тесты Стьюдента

Одной из часто встречающихся статистических проблем является проверка гипотез относительно математического ожидания исследуемых выборок. Существует целый ряд статистических тестов, называемых t-тестами Стьюдента, проверяющих различные гипотезы относительно математического ожидания.

t-тест для одной выборки Этот тест используется для проверки гипотезы о том, что математическое ожидание случайной величины X, представленной выборкой X_S , имеет заданное значение μ. Тест требует, чтобы переданная в него выборка являлась выборкой нормальной случайной величины. В процессе своей работы тест вычисляет t-статистику 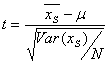.   Если величина X распределена нормально, то статистика t будет иметь распределение Стьюдента с N-1 степенями свободы. Это позволяет нам использовать распределение Стьюдента для определения уровня значимости, соответствующего полученному значению t-статистики.
t–тест для двух независимых выборок. Тест в данном случае проводится для сравнения средних значений по двум выборкам, в ситуации, когда результаты в выборках не могут быть «естественным образом сведены в пары» . В таких случаях нельзя сводить значения в одну группу, необходимо работать с двумя выборками. Расчет t – статистики для независимых выборок: 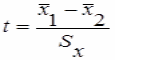,где 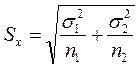- для выборок большого размера (более 30) имеет широкое применение на практике.   Для выборок малого размера (< 30): 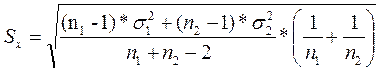   .    В дальнейшем t_стат и t_табл    сравниваются между собой и делается вывод о средних двух независимых выборок - если t_стат > t_табл , то отличии средних значимо.

В случае, если X не является нормальной случайной величиной, то величина t будет иметь другое, неизвестное распределение, и, строго говоря, t-тест Стьюдента нельзя применять. Однако в соответствии с центральной предельной теоремой при росте размера выборки распределение t будет стремиться к распределению Стьюдента. Таким образом, если размер выборки достаточно велик, то мы можем использовать t-тест, даже если требование нормальности распределения не выполняется. Однако не существует простого способа определить, N достаточно велико. В каждом конкретном случае есть своя граница, зависящая от того, насколько исследуемое распределение отклоняется от нормального. Некоторые источники приводят в качестве "достаточно большого N" 30, но даже этот размер выборки может оказаться недостаточен. Альтернативой в этом случае может являться непараметрический тест - критерий знаков или W-критерий Уилкоксона

Критерий знаков

Критерий знаков - это непараметрический тест, использующийся для сравнения медианы распределения с заданным значением m. Этот критерий может использоваться в качестве независимой от распределения альтернативы t-критерию Стьюдента для одной выборки требующему нормальности распределения. Критерий знаков предъявляет к тестируемой выборке только одно требование: шкала измерений должна быть порядковой, интервальной или относительной (т.е. тест нельзя применять к номинальным переменным). Других ограничений (в том числе и на форму распределения) нет. С одной стороны, это делает тест настолько широко применимым, насколько это вообще возможно. С другой - снижает его мощность, поскольку тест не может опираться в своей работе на какие-либо предположения о свойствах анализируемого распределения. Невысокая мощность критерия знаков особенно сильно проявляется на небольших выборках. Это является следствием того, что тест использует информацию только о положении элементов выборки относительно предполагаемой медианы: слева или справа. Информация об их сравнительной величине тестом не используется. В то же время, есть более мощный тест - W-критерий Уилкоксона, использующий информацию о ранге элементов в выборке. К сожалению, сфера применения этого теста ограничена распределениями, симметричными относительно медианы. Для несимметричных распределений он дает некорректные результаты, так что в нашем распоряжении остается только менее мощный критерий знаков.

Графическое изображение статистических данных.

Для наглядного представления наблюдаемых значений применяют графическое изображение статистического материала.
Часто для этого используют гистограммы и тренд.
Статистическим (эмпирическим) законом распределения выборки обьема N, или просто статистическим распределением выборки называют последовательность вариант X_i и соответствующих им частот N_i или относительных частот W_i. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот, в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал.

Гистограмма - один из вариантов столбиковой диаграммы, позволяющий зрительно оценить распределение статистических данных, группированных по частоте попадания в интервалы.
По виду гистограммы, по тому, на какой вид распределения плотности вероятности похожа гистограмма,
можно судить о теоретическом законе распределения.
В приложении принят следующий порядок расчета параметров гистограммы:
1.размах R = (X_min-X_max);   2.количество интервалов K= ~ 3.3*lg(N);
3.длина одного интервала H= ~ R/K;   4.начало первого интервала X₀= ~ X_min, последнего X_k=X₀+H*K.
Значок ~ означает, что равенство не точное, и результат подобран (например, с учетом зрительного восприятия).
Частоты попадания в интервал рассчитываются так: если X_i ~далеко от границ интервала,
то его относим к этому интервалу с весом 1; если X_i отстоит от границы не далее чем на e*H,
то относится к текущему и ближнему интервалу с весом 0.5.   e - коэффициент "принадлежности", задан может быть в пределах: 0.1 - 0.4.     В гистограмме с коэффициентом "принадлежности" 0.4 большинство значений будут принадлежать двум соседним интервалам.
Если случайные величины Y и X находятся в вероятностной зависимости, это означает,
что с изменением величины X величина Y имеет тенденцию также изменяться (например, возрастать или убывать при возрастании X). Эта тенденция соблюдается лишь «в среднем», в общих чертах.
Если значения случайной величины Y получены на последовательных равных промежутках (времени, пространства, ...), то для такой выборки можно проследить зависимость от номера отсчета. Эта характеристика будет показывать тенденцию изменения в среднем и часто называется трендом.
Тренды могут рассчитываться различными методами. Для определения возможной тенденции в последовательности данных можно воспользоваться линейным уравнения регрессии.

Аналитическое выравнивание и построение уравнения регрессии.

Регрессия – это линия, характеризующая наиболее общую тенденцию во взаимосвязи факторного и результативного признаков. Предполагается, что аналитическое уравнение выражает подлинную форму зависимости, а все отклонения от этой функции обусловлены действием различных случайных причин. Выбор функции должен опираться на знание специфики предмета исследования. Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
Чаще всего при аналитическом выравнивании используется метод наименьших квадратов(МНК), смысл которого заключается в следующем: вычисленные теоретические значения должны быть максимально близки к фактическим, т.е. сумма квадратов отклонений теоретических значений от фактических должна быть минимальна. Воспользовавшись этим принципом можно получить следующую систему нормальных уравнений для определения коэффициентов полинома третьей степени:  
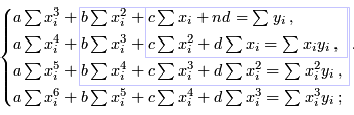
Из рисунка также видно как выглядят уравнения для полиномов второй и первой степени.
МНК используется для нахождения коэффициентов(параметров) и для других функций регрессии.

    Параметры уравнения регрессии   y = b·e^a·x+c    вычислялись в следующей последовательности:
1. отношение производных в точках i+1 и i равно e^a·dx_i откуда    a_i = ln(y^'_i+1 / y^'_i) / dx_i;   a считается средним по a_i.
2. dy_i = b·(e^a·x_i - e^a·x_i-1); отсюда определяются b_i   и b как среднее;
3. c_i = y_i - b·e^a·x_i , соответственно с это среднее.
4. если ошибка аппроксимации ~небольшая(например, меньше 1%), то расчеты заканчиваются, иначе, предполагая что параметр с определен достаточно точно, параметры a и b ~уточняем из уравнения y-c = b·e^a·x ,приводя его к линейному ln(y-c) = a·x + ln(b)    и используя МНК.
    При экспоненциальной регрессии (впрочем, и в других случаях тоже) для более достоверного оценивания параметров можно придерживаться следующих правил:    1. ~достаточное(>12) количество ИД;    2. ИД должны принадлежать разным областям функции (быстрое, среднее, слабое изменения);    3. значения x должны возрастать, ~лучше использовать постоянный шаг изменения x.

    Параметры уравнения гиперболической регрессии   y = 1/(a·x+b) +c    вычислялись ,примерно, в той же последовательности, что и параметры экспоненты.
Использовался инвариант W_i:   W_i= (x_i+1 - Z_i·x_i) / (Z_i-1) = b/a ,  где    Z_i= √(y'_i/y'_i+1)   и y' соответствующие производные.
Параметр a можно определить из уравнения:    a·dy_i= 1/(x_i+1+W_i) - 1/(x_i+W_i).
Так как производные оцениваются по ИД, то при больших отклонениях ИД от ~истинных или больших шагах по х, параметры также могут значительно отклоняться.
Можно отметить, что запись уравнения гиперболы в виде y = k/(a·x+b) +c    не дает ничего дополнительно по сравнению с ранее приведенным уравнением, так как k≠0, т.е. числитель и знаменатель можно разделить на k.

    Параметры уравнения трехзвенной ломаной    y₁ = a₁·x+b₁;   y₂ = a₂·x+b₂;    y₃ = a₃·x+b₃;   вычислялись в следующей последовательности:
1. Полагаем, что в звене 1 и 3 одинаковое количество точек и задаем их начальное количество равное 2.
2. Определяем параметры уравнений для такой конфигурации звеньев используя МНК. Находим среднюю ошибку аппроксимации.
3. Добавляем к звеньям 1 и 3 по одной соответствующей точке (из звена 2 эти точки убираются).
4. Определяем параметры уравнений для новой конфигурации звеньев используя МНК. Находим среднюю ошибку аппроксимации.
5. Пункты 3 и 4 выполняются для всех возможных конфигураций и поиска ~лучшей симметричной конфигурации с наименьшей ошибкой аппроксимации. Пусть количество точек в этой конфигурации будет: k11, k21, k31.
6. Для поиска возможной лучшей ~немного несимметричной конфигурации фиксируем количество точек в узле 1 (k11) и варьируем узел 3 (соответственно 2). Затем фиксируем количество точек в узле 3 (k13) и варьируем узел 1.   Конфигурация с наименьшей средней ошибкой аппроксимации и будет лучшей.